متوازي المستطيلات هو أحد الأشكال الهندسية ثلاثية الأبعاد التي تتميز بوجود ستة أوجه مستطيلة، وهو من أكثر الأشكال استخدام في الهندسة والرياضيات والحياة اليومية ويمكن العثور عليه في العديد من الأشياء المحيطة بنا، مثل الصناديق، الكتب، وقطع الأثاث، وسنتعرف على خصائص متوازي المستطيلات، عدد رؤوسه، شكله، وكيفية حساب مساحته وحجمه، بالإضافة إلى توضيح الفرق بينه وبين المكعب، مع أمثلة عملية تسهل فهمه.
متوازي المستطيلات
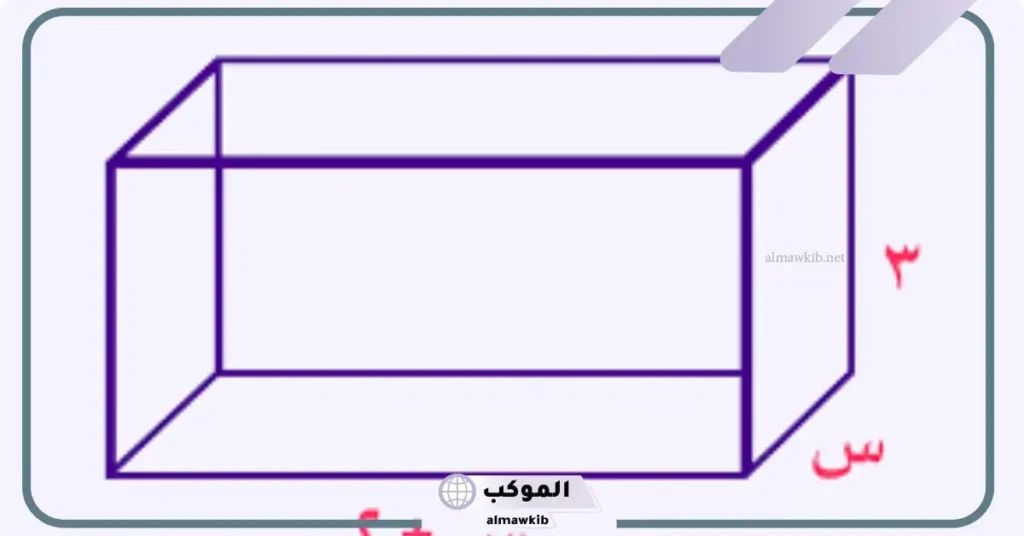
متوازي المستطيلات هو شكل هندسي ثلاثي الأبعاد له ستة أوجه، كل وجه منها على شكل مستطيل وتتميز الأوجه المتقابلة بأنها متطابقة ومتوازية، مما يجعله شكل منظم وسهل الحساب من حيث المساحة والحجم، ويعرف متوازي المستطيلات في اللغة الإنجليزية باسم Cuboid ويستخدم هذا المصطلح في الرياضيات والهندسة لوصف أي شكل له ستة أوجه مستطيلة، وهو يختلف عن المكعب (Cube)، حيث تكون جميع أبعاده متساوية.
عدد رؤوس متوازي المستطيلات
لمتوازي المستطيلات ثمانية رؤوس (Vertices)، وهي النقاط التي تتلاقى فيها ثلاث حواف كما يمتلك 12 حرف (Edges) و6 أوجه (Faces)، حيث تتصل هذه الأوجه بطريقة تجعل كل وجهين متقابلين متطابقين، وإذا اعتبرنا متوازي مستطيلات بأبعاد (طول = 8 سم، عرض = 5 سم، ارتفاع = 3 سم)، فسنجد أن رؤوسه تكون عند تقاطع الأبعاد الثلاثة في الفضاء أربعة رؤوس في القاعدة السفلى وأربعة رؤوس في القاعدة العلوية.
شكل متوازي المستطيلات
يتميز متوازي المستطيلات بأنه يمتلك ستة أوجه، وكل وجه عبارة عن مستطيل والأوجه المتقابلة متساوية في المساحة ومتوازية، وجميع الزوايا بين الأوجه تساوي 90 درجة، فإذا تساوت الأبعاد الثلاثة لمتوازي المستطيلات (الطول = العرض = الارتفاع)، فإنه يصبح مكعب، حيث تكون جميع الأوجه مربعات بدل من مستطيلات.
اقرأ أيضًا: قانون مساحة المربع
مساحة متوازي المستطيلات
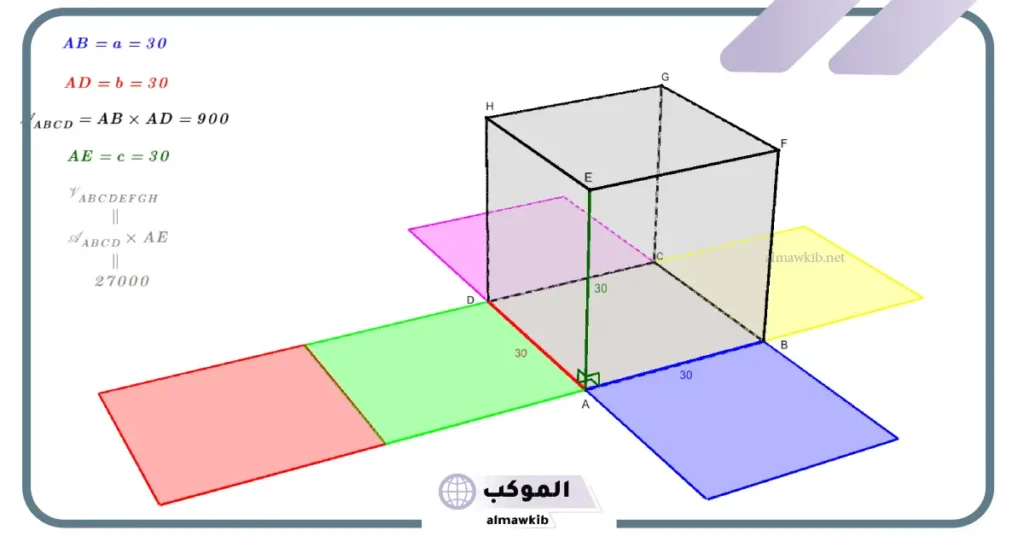
لحساب المساحة الكلية لمتوازي المستطيلات، نستخدم الصيغة التالية: المساحة الكلية=2×(الطول×العرض+الطول×الارتفاع+العرض×الارتفاع)
إذا كان لدينا متوازي مستطيلات بأبعاد: الطول = 10 سم والعرض = 5 سم والارتفاع = 4 سم
فإن المساحة الكلية له تكون: المساحة الكلية=2×(الطول×العرض+الطول×الارتفاع+العرض×الارتفاع)
أمثلة على متوازي المستطيلات
- الصناديق الكرتونية المستخدمة في التخزين والشحن.
- الكتب والمجلدات، حيث تتخذ شكل متوازي المستطيلات.
- قطع الأثاث مثل الخزائن والأدراج والصناديق.
- حاويات الشحن المستخدمة في نقل البضائع.
- الطوب المستخدم في البناء، حيث يكون في الغالب على شكل متوازي مستطيلات.
اقرأ أيضًا: محيط المربع ومساحته
حجم متوازي المستطيلات
لحساب حجم متوازي المستطيلات، نستخدم الصيغة التالية: الحجم=الطول×العرض×الارتفاع
إذا كان لدينا متوازي مستطيلات بأبعاد: الطول = 8 سم والعرض = 6 سم والارتفاع = 3 سم
فإن حجمه يكون: الحجم=8×6×3=144سم3
تعريف متوازي المستطيلات و المكعب
- متوازي المستطيلات هو شكل هندسي ثلاثي الأبعاد له ستة أوجه مستطيلة، وزواياه كلها قائمة (90 درجة).
- المكعب هو حالة خاصة من متوازي المستطيلات تكون فيها جميع الأبعاد متساوية، أي أن الطول = العرض = الارتفاع، مما يجعل جميع الأوجه مربعات بدلاً من مستطيلات.
خصائص متوازي المستطيلات
- يحتوي على ستة أوجه مستطيلة، كل وجهين متقابلين متطابقين ومتوازيين.
- له 12 حرف مستقيم، وهي الخطوط التي تربط بين الرؤوس.
- له 8 رؤوس، وهي نقاط التقاء الحواف.
- جميع زواياه قائمة (90 درجة).
- يمكن حساب مساحته وحجمه بسهولة باستخدام القوانين الرياضية.
يعد متوازي المستطيلات من الأشكال الهندسية الأساسية التي نجدها في العديد من التطبيقات اليومية والهندسية ويتميز بخصائصه الفريدة التي تسهل حساب مساحته وحجمه باستخدام قوانين بسيطة، مما يجعله ضروريًا في مجالات مثل التصميم، البناء، والتخزين ومن خلال فهم خصائصه وقوانينه، يمكننا تطبيقها عمليًا لحل العديد من المشكلات الرياضية والهندسية بسهولة.